Số chính phương là gì? Các số chính phương từ 1 đến 100

Nếu như bạn đang có nhu cầu tìm hiểu về số chính phương và chưa tìm được được nguồn tài liệu hữu ích thì hãy đọc bài viết này. Đây là bài viết chia sẻ chi tiết nhất về số chính phương từ định nghĩa, cách nhận biết và tính chất của số chính phương để giúp bạn hiểu rõ hơn.

I. Số chính phương là gì?

1. Định nghĩa

Số chính phương là số tự nhiên có căn bậc hai cũng là một số tự nhiên, có thể hiểu đơn giản số chính phương chính là bình phương của một số tự nhiên. 

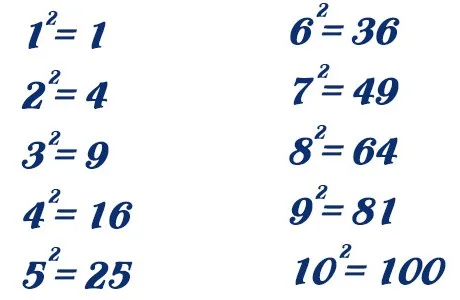
Ví dụ:

• 25(5)² và 16(4)² là các số chính phương.

Lưu ý: Số chính phương chẵn là bình phương của một số chẵn và ngược lại thì số chính phương lẽ là bình phương của một số lẽ.

2. Tính chất

Số chính phương có những tính chất sau đây:

• Số chính phương chỉ có chữ số tận cùng là 0, 1, 4, 5, 6, 9, nếu như các số có tận cùng là 2, 3, 7, 8 thì không phải là số chính phương.
• Số chính phương chỉ chứa các thừa số nguyên tố với số mũ chẵn.
• Số chính phương chỉ tồn tại 1 trong 2 dạng là 4n hoặc 4n + 1 (với n € N).
• Số chính phương chỉ tồn tại 1 trong 2 dạng là 3n hoặc 3n + 1 (với n € N).
• Số chính phương nếu như có chữ số tận cùng là 1 hoặc 9 thì chữ số hàng chục là chữ số chẵn.
• Số chính phương nếu như có chữ số tận cùng bằng 5 thì chữ số hàng chục là 2.
• Số chính phương nếu như có chữ số tận cùng bằng 4 thì chữ số hàng chục là chữ số chẵn.
• Số chính phương nếu như có chữ số tận cùng bằng 6 thì chữ số hàng chục là chữ số lẻ.
• Số chính phương nếu như chia hết cho 2 thì sẽ chia hết cho 4.
• Số chính phương nếu như chia hết cho 3 thì sẽ chia hết cho 9.
• Số chính phương nếu như chia hết cho 5 thì sẽ chia hết cho 25.
• Số chính phương nếu như chia hết cho 8 thì sẽ chia hết cho 16.
• Số chính phương nếu như chia cho 3 thì sẽ không bao giờ có số dư là 2.
• Số chính phương nếu như chi cho 4 thì không bao giờ có số dư là 2 hoặc 3.
• Số chính phương nếu lẻ khi chia cho 8 sẽ luôn dư 1

3. Đặc điểm của số chính phương

Công thức để tính hiệu của hai số chính phương

a² - b² = (a+b)(a-b)

Ví dụ:

• 6² – 3² = (6+3)(6-3) = 9.3 = 27.

Số ước nguyên dương của số chính phương là một số lẻ.

Ví dụ:

• Số chính phương 144 (12²) chia hết cho 3 (144:3=48) cho nên 144 chia hết cho 9 (144:9=16)

Số chính phương chia hết cho số nguyên tố p thì chia hết cho p².

Ví dụ:

• Số chính phương 36 (6²) chia hết cho 2 cho nên 36 chia hết cho 4 (2²)

Tất cả các số chính phương có thể viết thành dãy tổng của các số lẻ tăng dần từ 1 = 1, 4 = 1 + 3, 9 = 1 + 3 + 5, 16 = 1 + 3 + 5 + 7, 25 = 1 + 3 + 5 + 7 + 9, ...v.v

II. Một số ví dụ về số chính phương

Hiện nay khi học trung học cơ sở các em học sinh sẽ gặp các bài bài toán về số chính phương rất là nhiều. Dựa theo định nghĩa, tính chất và đặc điểm của số chính phương ta có những ví dụ về số chính phương để các bạn tham khảo như sau:

• 4 = 2² là một số chính phương chẵn
• 9 = 3² là một số chính phương lẻ
• 16 = 4² là một số chính phương chẵn
• 25 = 5² là một số chính phương lẻ
• 36 = 6² là một số chính phương chẵn
• 225 = 15² là một số chính phương lẻ
• 289 = 17² là một số chính phương lẻ
• 576 = 24² là một số chính phương chẵn
• 1.000.000 = 1.000² là một số chính phương chẵn

Như vậy có thể thấy các số 4, 9, 16, 25, 36, 225, 289, 576 và 1.000.000 đều là những số chính phương. Ngoài ra còn có rất nhiều số chính phương khác, các bạn có thể tự suy nghỉ và tự cho ví dụ nhé.

Bài viết nên đọc

• Số hữu tỉ là gì? Số vô tỉ là gì?